All About Option Greek-Delta

What is Delta in options? The first of the option Greeks, Delta, measures the change in the option price due to a change in the underlying’s price. Delta in options can be mathematically denoted as a change in the price of an option/change in the price of the underlying. Since options are derivative instruments, one must have an idea of how much an option price moves to a change in the price of the underlying asset. Call options increase with the price increase and have a positive delta, whereas put options increase with a fall in prices and have a negative delta.

In other words, call prices have a positive correlation with the underlying, while put prices have a negative correlation with the underlying. Typically, deltas are not followed by a decimal. A call option with a delta of 0.20, for instance, would be called a 20-delta call. A 20-delta put is one whose put delta is less than 0.20.

Example: Let us consider a call option of Nifty with a strike price of 17,500 at a premium of Rs 90 and a delta of 0.60. The spot price of the Nifty is at 17,534. This means if the spot moves up by Rs 50 the call option will move by Rs 30 (Rs 50 x 0.60 = Rs 30) to Rs 90.

Let us take another example for a put option with a strike price of 17,600 at a premium of Rs 116 and a delta of 0.61. If the spot drops by Rs 50, then the option price would increase by Rs 30.5 (Rs 50 x 0.61) to Rs 146.50

Delta is often used by traders to predict whether an option will expire in the money.

The underlying prices, implied volatility and the time to expiry are the factors that impact the delta.

Delta and call options

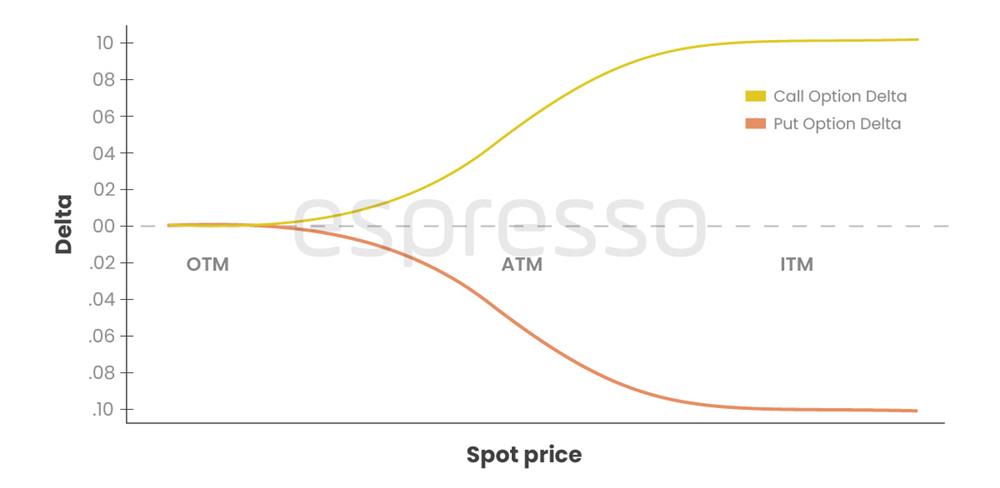
Delta for call options ranges from 0 to 1. At-the-money call options have a delta close to 0.50, meaning they have a 50 per cent chance of expiring in the money. For example, the August 2022 end Nifty at-the-money call having a delta of 0.48 has a 48 per cent chance of ending in the money.

In-the-money call options have a delta between 0.50 and 1. Deeper-in-the-money strikes have a delta close to 1 as it is already in the money and the chances of expiring in-the-money are also very high.

Out-of-the-money calls have a delta of 0 to 0.50. Out-of-the-money call options have no intrinsic value and are, therefore, less sensitive, and the chances of expiring in the money are very less. Deep out-of-the-money calls have a delta close to zero.

Delta and put options

Delta for put options ranges from -1 to 0.

At-the-money put options have a delta close to -0.50, meaning they have a 50 per cent chance of expiring in the money. For example, the August 2022 end Nifty at-the-money call of delta 0.52 has a 52 per cent chance of ending in the money.

In-the-money put options have a delta between 1 and 0.50. Deeper-in-the-money strikes have a delta close to 1 as it is already in the money, and the chances of expiring in the money are also very high.

Out-of-the-money puts have a delta of 0.50 to 0. Out-of-the-money call options have no intrinsic value and are, therefore, less sensitive, and the chances of expiring in the money are very less. Deep out-of-the-money calls have a delta close to zero.

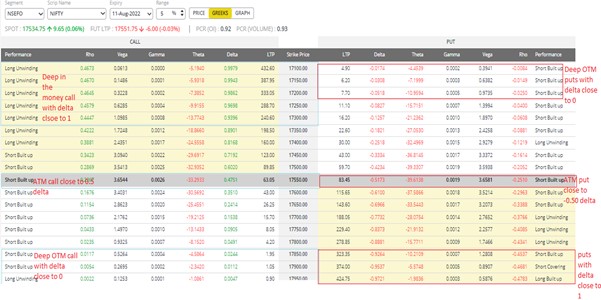
The following Nifty option chain clearly shows how the delta is highest for in-the-money options and lowest for out-of-the-money options. The delta keeps dropping as it moves from in-the-money to out-of-the-money. Delta moving from out-of-the-money to at-the-money is maximum, and from at-the-money to in-the-money slowly flattens for both calls and puts.

The above changes in the delta can be easily understood with the chart of delta and moneyness below.

Time to expiry and volatility

Volatility and time to expiry also impact option delta. The amount of time left until expiration will also impact Delta. An in-the-money call with a longer period until expiration than a call with the same strike and a shorter time until expiration will always have a smaller Delta. In contrast, for out-of-the-money calls, the call with the longer time to expiration will have a higher delta than the option with a shorter remaining time. If all other inputs remain constant, as expiry draws closer, in-the-money call deltas rise toward 1, at-the-money call Deltas stay around 0.50, and out-of-the-money call deltas decrease toward zero.

Also, with an increase in implied volatility, the delta tends to migrate toward 0.50 as more and more strikes are now seen as having a chance of moving in-the-money due to the perceived possibility of movement in the underlying. On the other hand, a decrease in volatility pushes out-of-the-money calls and puts towards zero, in-the-money call delta towards 1, and in-the-money put delta towards -1.

Conclusion

Delta is useful for small price moves. For larger price moves, we need to understand gamma. Gamma also changes with the change in prices of the underlying. As we know, delta is the speed, and gamma is the acceleration. We shall deal with gamma in the next chapter.

Things to remember

• Option Greek, Delta, measures the change in the option price due to a change in the underlying’s price.
• Delta is mathematically denoted as a change in the price of an option/change in the price of the underlying.
• Call options to increase with the price increase and have a positive delta, whereas put options increase with a fall in prices and have a negative delta.
• Deltas are not followed by a decimal. A call option with a delta of 0.20 would be called a 20-delta call. A 20-delta put is one whose put delta is less than 0.20.
• Delta is useful for small price moves. For larger price moves, it’s the gamma.