Using Greek calculators

As a trader, one needs to keep track of positions keenly. While it is relatively easy to monitor a stock portfolio, it is not simple to keep track of option positions.

Option positions are dynamic, unlike stocks. Stocks can be bought and held for variable durations. However, options are derived from the prices of stocks and decay over their specified life, a process known as expiration. Monitoring an option position thus becomes more intense.

Options trading cannot be compared to stock trading. In stock trading, one can buy shares based on technical analysis and fundamental analysis. Options trading, on the other hand, is a different ball game.

The Greeks

In stock trading, one only has to monitor the share price, but in options trading, apart from the price of the underlying security, one has to also monitor other elements known as the Greeks.

The Greeks are mathematically derived values using option-pricing models.

The major Greeks are delta, gamma, theta, and vega. Delta and gamma predict option price movement in response to changes in the underlying asset's price. Theta is an estimate of how much the extrinsic value of an option will drop after one day. Vega indicates how options prices will react to changes in volatility.

There are many option-pricing models, but we will use the most popular one, known as the Black-Scholes model.

Inputs and output

To get a result from the Greeks, an Option Greeks calculator has to be fed with the following information:

Spot price: The current market price of the underlying stock or index.

Strike price: The price at which the option holder gets the right to buy the underlying security in case of a call and the right to sell in case of a put.

Days to expiry: The number of days to the contract's expiration. The days to expiry are input as a number in the option greeks calculator.

Interest: Interest rates impact options pricing. The risk-free interest rate is used to arrive at options pricing. The interest rate is to be input as a percentage in the option greeks calculator.

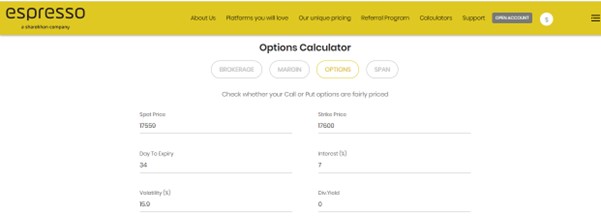Volatility: Volatility impacts both call and put options alike. An increase in volatility causes all option prices to rise, and a decrease in volatility leads to a drop in option prices. Volatility is also input as a percentage in the option greeks calculator.

Dividend yield: As companies declare dividends, stock prices fall to the extent of the dividend declared on the ex-dividend date. However, option prices are adjusted in anticipation even before or when a dividend is declared. Call prices drop and put prices rise in anticipation of the drop in the stock’s price due to dividends. The dividend yield is also input as a percentage in the option greeks calculator.

After these variables are entered and the option greeks calculator tab is hit, we get the following output of the Greeks:

Delta: The delta of both the call and the put for the selected strike is displayed. Delta measures the sensitivity of an option’s price change to the change in the price of the underlying asset. It is a percentage of the underlying price displayed in decimals.

Gamma: Gamma is the sensitivity of delta to the change in the price of an underlying asset. Gamma measures the expected change in delta for a change in the underlying asset.

Vega: Vega measures the sensitivity of the option to changes in volatility measured in percentage.

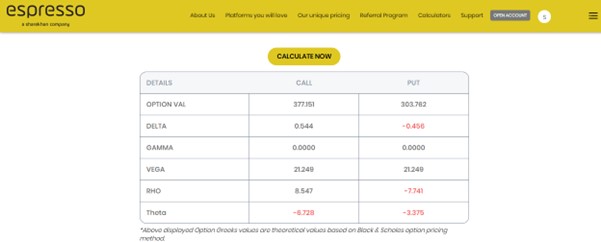RHO: RHO measures the change in option prices due to a change in the interest rate. Option prices are sensitive to an increase or decrease in risk-free interest rates.

Theta: All options are bound by time. They have a time value that decays as expiration nears. Theta measures the time decay of an option in rupee terms per day as expiration nears.

The option value is displayed for the call and the put is the theoretical value of the option. This needs to be compared with the actual option value to check if the option is expensive or cheap. However, one must be sure about the inputs.

Points to remember:

• Option Greeks are important factors to consider and monitor while trading options.
• The most popular options pricing model is known as Black-Scholes.
• Delta and gamma predict changes in price in relation to changes in the underlying asset. Theta indicates time decay. Vega signifies the relationship between the option price and volatility.